Soru
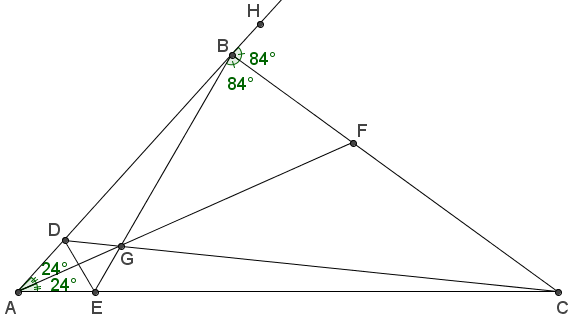
Şekildeki \(ABC\) üçgeninde, \([CD] \cap [BE] \cap [AF] = \left\{ G \right\}\), \(m(\widehat {BAF}) = m(\widehat {CAF}) = {24^ \circ }\), \(m(\widehat {CBE}) = m(\widehat {CBH}) = {84^ \circ }\) ve \(A\), \(B\) , \(H\) doğrusal olduğuna göre, \[m(\widehat {CDE})\] kaç derecedir?
Çözüm 1 - Temel GÖKÇE
Buradan \[|CE| = \frac{{|CA|.|BE|}}{{|BA|}}\] elde edilir. \(\triangle ABC\) ninde \([AF]\) iç açıortay olduğundan \(\dfrac{{|CA|}}{{|AB|}} = \dfrac{{|CF|}}{{|BF|}}\) dir.
Buradan \[|BF| = \frac{{|AB|.|CF|}}{{|CA|}}\] olur.
\(\triangle ABC\) ninde Seva teoremi uygulanırsa \[\frac{{|CE|}}{{|EA|}}.\frac{{|AD|}}{{|DB|}}.\frac{{|BF|}}{{|FC|}} = 1\] olur. Yukarıda bulduğumuz eşitlikleri yerine yazarsak \[\frac{{|CA|.|BE|}}{{|BA|.|EA|}}.\frac{{|AD|}}{{|DB|}}.\frac{{|AB|.|CF|}}{{|FC|.|CA|}} = 1\] olur. Sadeleştirmeler yapılırsa \[\frac{{|BE|}}{{|EA|}} = \frac{{|DB|}}{{|AD|}}\] elde edilir. O halde \([ED]\), \(\triangle AEB\) nin iç açıortayıdır. Bu durumda \(m(\widehat {AEG}) = {120^ \circ }\) olduğundan \[m(\widehat {AED}) = m(\widehat {DEB}) = m(\widehat {BEC}) = {60^ \circ }\] olur.
Demek ki \([EB]\) de \(\triangle ADE\) nin dış açıortayıdır. Bu üçgende \([AF]\) de iç açıortay olduğundan \([DC]\) de dış açıortay olur. Böylece \[m(\widehat {CDE}) = {54^ \circ }\] bulunur.
Çözüm 2 - Süleyman SÖYLER
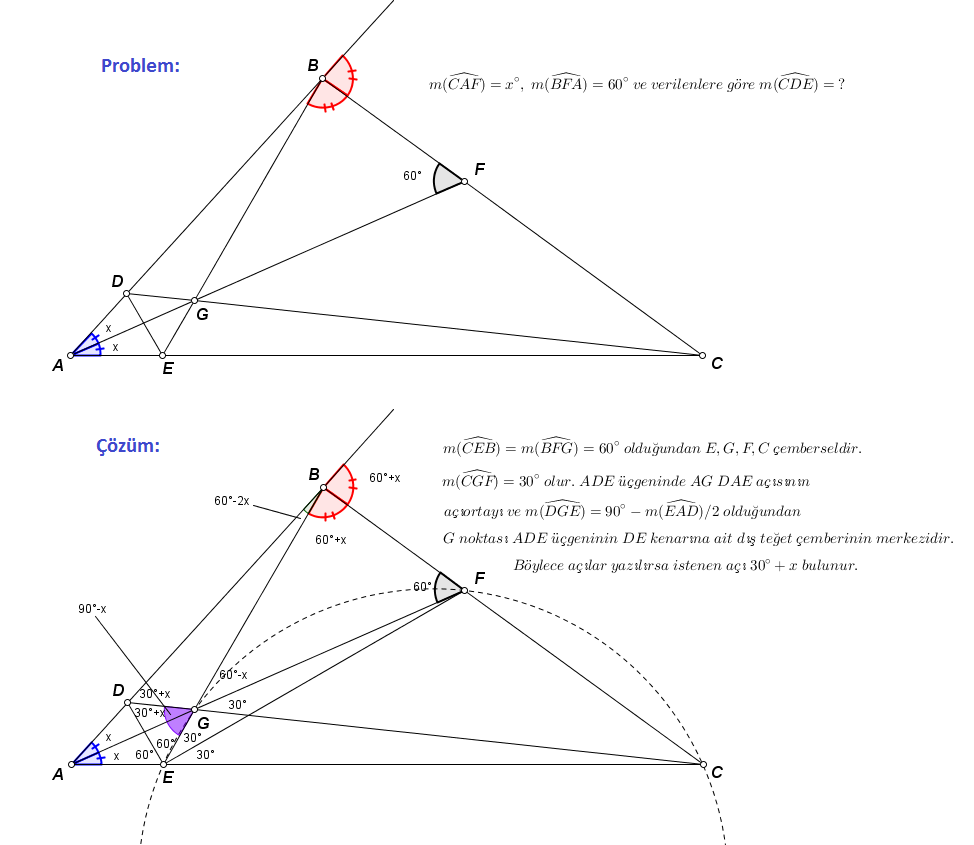
Çözümler için Temel GÖKÇE ve Süleyman SÖYLER öğretmenlerime teşekkür ediyorum.
Sorunun özünde \(\triangle AEB\) nin \(A\) ve \(E\) köşelerinden çıkan iç açıortaylarının sırasıyla kenarları kestiği noktalar olan \(G\) ve \(D\) ile, \(B\) köşesinden çıkan dış açıortayının \(AE\) yi kestiği nokta olan \(C\) nin daima doğrusal olması yatıyor. Bunun ispatı, 1. çözümde geçen yöntemle yapılabilir.

