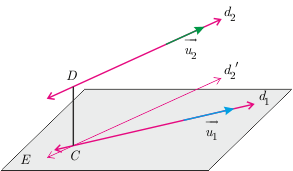
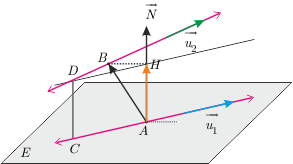
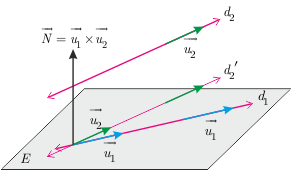
O halde aykırı iki doğru arasındaki en kısa uzaklık $$|AH|=\dfrac{\left |<\overrightarrow{AB},\overrightarrow{N}> \right |}{||\overrightarrow{N}||}=\dfrac{\left |<\overrightarrow{AB},\overrightarrow{u_1}\times\overrightarrow{u_2}> \right |}{||\overrightarrow{u_1}\times\overrightarrow{u_2}||}$$ olur.
Şeklin Cabri versiyonu için tıklayın!
Örnek 1
\({d_1}:\dfrac{{x - 1}}{2}=y + 1=- z\) ve \({d_2}:\dfrac{{x + 1}}{3}=- y=\dfrac{{z - 1}}{2}\) doğruları arasındaki en kısa mesafe kaç birimdir?
Çözüm
\(d_1\) doğrusunun geçtiği sabit nokta \(A(1,-1,0)\) ve doğrultu vektörü \(\overrightarrow {{u_1}} = (2,1, - 1)\); \(d_2\) doğrusunun geçtiği sabit nokta \(B(-1,0,1)\) ve doğrultu vektörü \(\overrightarrow {{u_2}} = (3, - 1,2)\) dir. Bu durumda \(\overrightarrow {AB} = ( - 2,1,1)\) olacaktır. Bu üç vektörün belirttiği determinantın değeri \(0\) dan farklı olduğundan lineer bağımsızdırlar. Bu nedenle doğrular aykırı doğrulardır (Bir önceki derste bu konu işlendi). Öncelikle \[\overrightarrow {{u_1}} \times \overrightarrow {{u_2}} = \left| {\begin{array}{*{20}{c}}{\overrightarrow {{e_1}} }&{\overrightarrow {{e_2}} }&{\overrightarrow {{e_3}} }\\2&1&{ - 1}\\3&{ - 1}&2\end{array}} \right| = (1, - 7, - 5)\] dir. O halde iki doğru arasındaki en kısa uzaklık \[\begin{array}{l}d({d_1},{d_2}) = \dfrac{{| < \overrightarrow {AB} ,\overrightarrow {{u_1}} \times \overrightarrow {{u_2}} > |}}{{||\overrightarrow {{u_1}} \times \overrightarrow {{u_2}} ||}}\\\\ = \dfrac{{| - 2.1 + 1.( - 7) + 1.( - 5)|}}{{\sqrt {{1^2} + {7^2} + {5^2}} }}\\ = \dfrac{{14}}{{5\sqrt 3 }}\end{array}\] bulunur.
Örnek 2
\({d_1}:x + 2y = 2;\;z = 0\) ve \({d_2}:x = 2z;\;y = 0\) doğrularının birbirine en yakın olan noktalarını bulunuz.
Çözüm
\(d_1\) doğrusunun geçtiği sabit nokta \(A(0,1,0)\) ve doğrultu vektörü \(\overrightarrow {{u_1}} = (-2,1,0)\);
\(d_2\) doğrusunun geçtiği sabit nokta \(B(0,0,0)\) ve doğrultu vektörü \(\overrightarrow {{u_2}} = (2,0,1)\) dir.
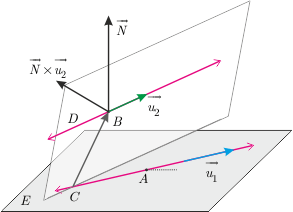
Ayrıca \(\overrightarrow {AB} = (0, - 1,0)\) ve \(\overrightarrow N = \overrightarrow {{u_1}} \times \overrightarrow {{u_2}} = (1,2, - 2)\) dir. Konu anlatımında olduğu gibi \(d_1\) doğrusunun \(d_2\) doğrusuna en yakın noktası \(C\) ve \(d_2\) doğrusunun \(d_1\) doğrusuna en yakın noktası \(D\) olsun. İki vektöre daha ihtiyacımız var: \[\overrightarrow N \times \overrightarrow {{u_1}} = (2,4,5)\] ve \[\overrightarrow N \times \overrightarrow {{u_2}} = (2, - 5, - 4)\] olur.
O halde bir \(k\in R\) için \[\begin{array}{l} < \overrightarrow {AB} - k\overrightarrow {{u_1}}\; ,\;\overrightarrow N \times \overrightarrow {{u_2}} > = 0\\ \Rightarrow k = - \dfrac{5}{9}\end{array}\] bulunur. Böylece \[C = A + k\overrightarrow {{u_1}} = (0,1,0) - \dfrac{5}{9}( - 2,1,0) = \left( {\dfrac{{10}}{9},\dfrac{4}{9},0} \right)\] olur.
Benzer biçimde bir \(m\in R\) için \[\begin{array}{l} < \overrightarrow {BA} - m\overrightarrow {{u_2}}\; ,\;\overrightarrow N \times \overrightarrow {{u_1}} > = 0\\ \Rightarrow m = \dfrac{4}{9}\end{array}\] bulunur. Böylece \[D = B + m\overrightarrow {{u_2}} = (0,0,0) + \dfrac{4}{9}( 2,0,1) = \left( {\dfrac{{8}}{9},0,\dfrac{4}{9},} \right)\] olur.
